Ilha de Koch

Neste artigo abordaremos resumidamente as figuras geométricas conhecidas como linha de Koch e ilha de Koch. O nome vem do matemático sueco Helge von Koch, que em 1904 referiu num artigo pela primeira vez a curva que é hoje conhecida como linha de Koch.

Linha de Koch

A linha de Koch é uma figura geométrica que nos será útil para definir a ilha de Koch. Consideremos a sequência de figuras que descrevemos em seguida. Partimos de um segmento horizontal, com uma unidade de comprimento.

Ponto de partida para a construção da linha de Koch.

Começamos por dividir este segmento em três partes iguais e substituimos a parte do meio por outros dois segmentos correspondendo a dois lados de um triângulo equilátero. Este passo está ilustrado na figura em baixo. O comprimento de cada um destes 4 segmentos é 1/3 pelo que o comprimento da linha completa é de 4/3.

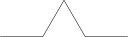
Primeira iteração da construção da linha de Koch.

No segundo passo fazemos algo semelhante ao realizado no primeiro passo, agora para cada um dos 4 segmentos da figura. Cada segmento é dividido em três e a parte do meio substituida por outros dois segmentos formando dois lados de um triângulo equilátero. Se no primeiro passo a figura era composta por segmentos de comprimento 1/3 agora os segmentos são de comprimento 1/9 e o comprimento total passou a ser 16/9.

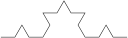
Segunda iteração da construção da linha de Koch.

As figuras em baixo correspondem aos passos 3, 4 e 5 deste processo.

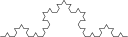
Iterações 3, 4 e 5 da construção da linha de Koch.

Continuando com o mesmo procedimento em cada passo, no limite obtém-se a figura designada por linha de Koch. Assumimos, sem demonstração, que existe efectivamente o limite desta sucessão.

A linha de Koch tem, entre outras, as seguintes propriedades interessantes:

• É uma linha contínua.
• Não tem derivada em nenhum ponto. Tomamos aqui a linha como uma aplicação de $\mathbb{R} \to \mathbb{R}^2$.
• Tem comprimento infinito.

É simples verificar que o comprimento da linha de Koch é infinito. De facto, se chamarmos $L_n$ ao comprimento da figura do passo $n$ tem-se que

$$L_n = \frac{4}{3}L_{n-1}$$

Como $L_0=1$ então

$$L_n = \left(\frac{4}{3}\right)^n,$$

que é uma sucessão que cresce sem ter majorante. Ou seja, o comprimento da figura limite é infinito.

Ilha de Koch

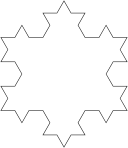
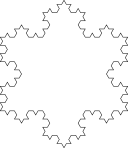
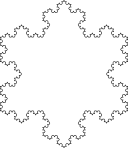
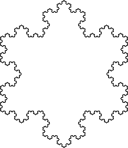
A figura conhecida como ilha de Koch é obtida através de um procedimento semelhante ao usado para criar a linha de Koch, mas em vez de começar com um único segmento começa-se com um triângulo equilátero. As imagens em baixo representam as seis primeiras iterações do procedimento.

A figura inicial e as cinco primeiras iterações da construção da ilha de Koch.

O perímetro da ilha de Koch é infinito. Tal acontece porque esta figura é constituida pela união de três versões idênticas, apropriadamente rodadas e deslocadas, da linha de Koch. No entanto a área da ilha de Koch é claramento limitada. Podemos mesmo calcular a área como o limite da sucessão das áreas das figuras intermédias.

A área da ilha de Koch pode ser obtida como o limite das áreas das figuras intermédias. Vamos então calcular a área $A_n$ da figura do passo $n$. A área da figura do passo $n$ é dada pela soma da área da figura do passo $n-1$ com as áreas dos pequenos triângulos que são adicionados à figura do passo $n-1$ para obter a figura do passo $n$.

Precisamos de saber quantos pequenos triângulos são acrescentados no passo $n-1$ para obter a figura do passo $n$. Precisamos também de saber o comprimento do lado desses pequenos triângulos, para calcular a respectiva área.

O número de pequenos triângulos que são acrecentados no passo $n-1$ corresponde ao número de troços no passo $n-1$. Chamemos $c_n$ ao número de troços no passo $n$. Tem-se então:

$$c_0=3, \quad c_n=4c_{n-1} \qquad \Rightarrow \qquad c_n = 3\times 4^n$$

O comprimento do lado dos pequenos triângulos que são acrescentados no passo $n-1$ corresponde ao número de troços que existem no passo $n$. Chamemos-lhe $l_n$. Tem-se que:

$$l_0=1, \quad l_n=\frac{1}{3}l_{n-1} \qquad \Rightarrow \qquad l_n = \left(\frac{1}{3}\right)^n$$

Chamemos $a_n$ à área de cada um dos pequenos triângulos acrescentados no passo $n-1$. Sendo a área a de um triângulo equilátero de lado $l$ dada por $a=\frac{\sqrt{3}}{4}l^2$ teremos

$$a_n = \frac{\sqrt{3}}{4} l_n^2 = \frac{\sqrt{3}}{4} \left(\frac{1}{9}\right)^n$$

Com o que já foi dito temos

$$A_n = A_{n-1} + c_{n-1}a_n$$ $$A_n = A_0 + \sum_{k=1}^n c_{k-1}a_k$$ $$A_n = \frac{\sqrt{3}}{4} \left( 1 + \frac{3}{4} \sum_{k=1}^n \left(\frac{4}{9}\right)^n \right)$$

No limite temos a soma dos termos de uma progressão geométrica de razão $\frac{4}{9}$. Sendo $\sum_{k=0}^\infty = \frac{1}{1-r}$, ou $\sum_{k=1}^\infty = \frac{r}{1-r}$, teremos finalmente a área $A$ da ilha de Koch como $$A = \lim A_n = \frac{2\sqrt{3}}{5}$$

Cólofon

As imagens PNG usadas neste artigo com os diferentes passos das iterações da linha de Koch e ilha de Koch foram geradas com Inkscape a partir de ficheiros SVG. Os ficheiros SVG com as figuras foram gerados a partir de um programa para geração de iterações de Sistemas-L escrito na linguagem de scripting Tea.