Neste artigo iremos falar de forma muito introdutória sobre poliominós e como se relacionam com dobragens de cubos.
Introdução
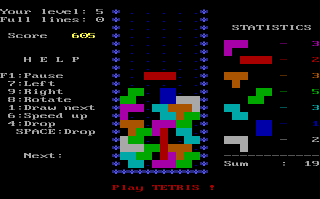
Poliominós são figuras geométricas compostas por quadrados. Cada quadrado é adjacente a um ou mais quadrados pelos lados. O número de quadrados que formam o poliominó corresponde ao seu grau. O jogo Tetris faz uso de poliominós. A imagem em baixo mostra o estado do jogo num instante arbitrário. As peças do jogo são poliominós de grau quatro, ou seja, cada peça é composta por quatro quadrados.
|
| Tetris game screenshot. |
Note-se que entre os poliominós do Tetris existem dois pares em que as figuras podem ser obtidas uma da outra através de uma reflexão. As peças B, C e as peças D, E podem ser obtidas uma da outra através de uma reflexão.

|
| Os poliominós de grau quatro que correspondem às peças do jogo Tetris. |
Existem duas classes comuns de classificação de poliominós. Poliominós de lado único e poliominós de forma livre.
- Poliominós do lado único --- São poliominós que não podem ser obtidos uns dos outros por qualquer composição de rotações. As figuras do Tetris formam o conjunto dos poliominós de grau quatro de lado único.
- Poliominós de forma livre --- São poliominós que não podem ser obtidos uns dos outros por qualquer composição de rotações e reflexões.
Geração de Poliominós
A geração de poliominós é extremamente simples. Dados os poliominós de grau \(n-1\) podem obter-se todos os poliominós de grau \(n\). O procedimento para a obtenção de todos os poliominós de grau \(n\) é pois recursivo. O processo tem início com o único poliominó de grau 2, formado por dois quadrados.
O procedimento para obtenção dos poliominós de grau \(n\) envolve tratar cada um dos poliominós de grau \(n-1\) da forma descrita em seguida.
Dado um poliominó de grau \(n-1\) são gerados poliominós de grau \(n\) adicionando à figura um novo quadrado em cada uma das posições possíveis. Na imagem em baixo está ilustrado este processamento. A figura cinzenta representa o poliominó original. O quadrado vermelho representa o quadrado que é adicionado à figura original em cada uma das posições possíveis.

|
| Geração de poliominós de grau \(n\) a partir de um poliominó de grau \(n-1\). |
Para cada um dos poliominós assim obtidos determina-se se devem ser adicionados à lista de poliominós de grau \(n\) encontrados até ao momento. Para tal verifica-se se o poliominó pode ser obtido de um dos poliominós já encontrados. Se estamos a gerar poliominós de lado único verifica-se se pode ser obtido de rotações. Se estamos a gerar poliominós de forma livre verifica-se se pode ser obtido por uma composição de rotações e reflexão.
Exemplos de Poliominós
Vamos de seguida apresentar os conjuntos de poliominós de forma livre até ao grau 7.
Monominós
Poliominós de grau 1 (monominós) são compostos por um único quadrado. Destes, obviamente, existe apenas um.
Dominós
Existe também apenas um único poliominó de grau 2, composto por dois quadrados.
Triminós
Poliominós de grau 3 são também designados por triminós, dos quais existem apenas 2.

|
| Triminós. |
Tetrominós
Os poliominós de grau 4 são as peças do jogo Tetris. Existem 5 na forma livre, visíveis na figura seguinte.

|
| Tetrominós. |
Pentominós
Outra designação dos poliominós de grau 5. Existem 12 deles.
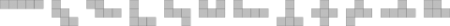
|
| Pentominós. |
Hexominós
Existem 35 poliominós de grau 6 distintos.

|
| Hexominós. |
Heptominós
Existem 108 poliominós de grau 7.

|
| Heptominós. |
Dobragens de Cubos
Alguns dos poliominós de grau 6 são dobragens de cubo. Por dobragem de cubo entendemos uma figura que por meio de dobragens apropriadas possa transformar-se num cubo. Cada dobragem individual tem sempre como eixo um lado de um dos quadrados que formam o hexaminó. Não é permitido "rasgar" a figura em qualquer um dos passos das dobragens.
As imagens seguintes ilustram um exemplo da dobragem de um cubo a partir de um hexominó. Cada imagem corresponde a um passo da sequência de dobragens desde a figura plana inicial (o hexominó) até chegar ao cubo.

|

|

|

|

|

|
| Os passos da dobragem de um cubo a partir de um hexaminó. | ||
Todos os poliominós de grau 6 de forma livre que correspondem a dobragens de um cubo estão indicados na figura em baixo.

|
| Hexominós que correspondem a dobragens de um cubo. |
Estes hexominós foram encontrados inspeccionando visualmente cada um dos 35 hexominós de lado único. A questão que vamos deixar no ar é se existirá algum algoritmo que permita classificar de forma simples um dado hexominó como sendo, ou não, uma dobragem de cubo. Ou, de forma quase equivalente, qual o algoritmo que permite gerar todos os hexominós que são dobragens de um cubo. Esperamos ter resultados para um artigo futuro.
Referências
Cólofon
As imagens PNG usadas neste artigo com figuras de poliominós foram geradas com Inkscape a partir de ficheiros SVG.
Os ficheiros SVG com figuras de poliominós foram gerados a partir de um programa para geração de poliominós escrito na linguagem de scripting Tea.
No comments:
Post a Comment